The choice of method for measuring laser linewidth depends on the intrinsic linewidth of the laser under test (LUT). A conventional approach is the heterodyne technique, which involves mixing two lasers and measuring the linewidth of the resulting RF or microwave beat frequency using an electronic signal or spectrum analyzer. This measurement reflects the combined linewidth contributions of both lasers.

Another widely used method is self-heterodyne detection, where the LUT signal is mixed with a frequency-shifted version of itself. This is achieved by sending the signal through an optical delay arm that must be longer than the coherence length of the LUT.

More recently, advances in homodyne frequency discrimination techniques have enabled ultra-narrow linewidth measurements. By analyzing phase and frequency noise, this method has demonstrated practical capability in resolving extremely small linewidths with high precision.

Laser linewidth reflects the fundamental noise characteristics of a laser. It is primarily determined by spontaneous emission noise, the output power, and the quality factor (Q) of the laser cavity, as described by the well-known Schawlow–Townes formula.

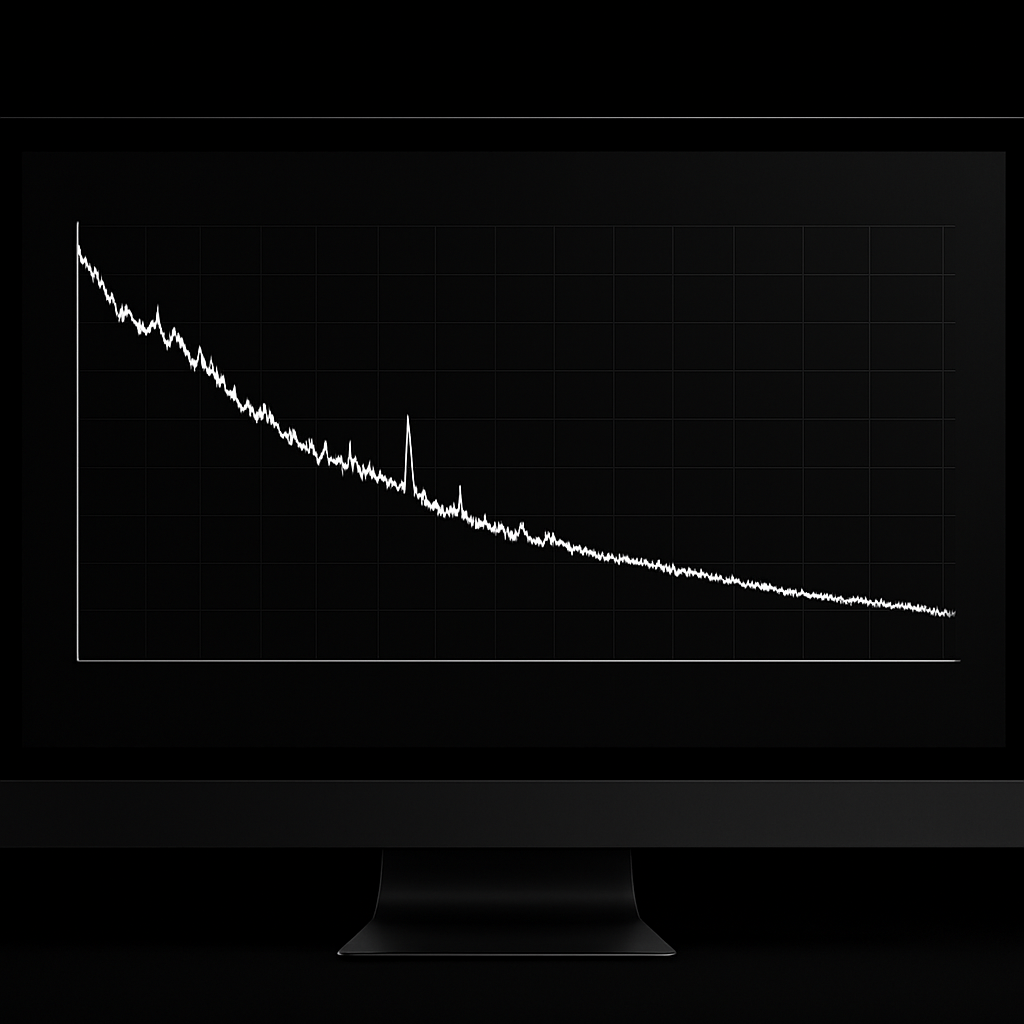
On a power spectral density (PSD) plot of frequency noise versus Fourier frequency, the laser linewidth corresponds to the white-noise segment. In this context, frequency noise refers to the total integrated noise represented in the PSD of the laser’s frequency fluctuations.

Modern measurement techniques often rely on phase and frequency noise analysis, which makes it possible to accurately determine linewidth by quantifying and integrating the noise contributions across the spectrum.

Phase noise and frequency noise are sometimes used interchangeably to describe the spectral noise of a laser, although they are expressed in different but related units. Both describe the signal source’s frequency and phase instability, and they are mathematically connected since frequency is the time derivative of phase.

‍Phase noise is typically expressed in units of dBc/Hz or rad²/Hz, while frequency noise is reported in units of Hz²/Hz or Hz/√Hz.

For certain applications, such as locking a laser to an external cavity or an atomic transition, the power spectral density of the phase noise is particularly important. It provides a way to determine the widest possible locking bandwidth and ensures optimal stability in precision applications.

Laser linewidth is directly related to the coherence length of the laser, which is the distance over which the light can propagate while maintaining phase coherence. In other words, it defines how far the wave can travel before its phase relationship begins to break down.

The coherence length is essentially given by the inverse of the linewidth, multiplied by the speed of light in the propagation medium. Depending on the medium—such as free space or optical fiber—this determines how long the laser signal can remain coherent without significant phase degradation.

The intrinsic linewidth of a laser arises from its fundamental spontaneous emission noise, which produces a Lorentzian spectral line shape as described by the Schawlow–Townes linewidth. This linewidth is considered a measure of the laser’s spectral purity and is sometimes referred to as the instantaneous linewidth, since it excludes contributions from technical noise sources such as environmental temperature fluctuations or mechanical vibrations.

Intrinsic linewidth is typically evaluated over short measurement time scales and represents the laser’s fundamental noise floor. Although it does not account for longer-term technical noise, it is often (perhaps unfortunately) the figure of merit specified for single-frequency laser sources.

Many active electronic and photonic devices exhibit flicker-like noise (1/fᵅ, where α > 2), which arises from instabilities in driver electronics as well as thermal and vibration effects in resonant cavities. This type of noise dominates at the lower Fourier frequencies of the noise spectrum, while fundamental noise sources such as spontaneous emission and shot noise dominate at higher frequencies.

The presence of 1/f noise significantly impacts the observed laser linewidth. Instead of a purely Lorentzian line shape (associated with spontaneous emission noise), the line shape transforms toward a Gaussian profile, with its numerical value dependent on the measurement time scale. In practice, neither the Lorentzian nor the Gaussian alone fully captures the true laser linewidth. A more accurate description is given by the Voigt profile, which represents the convolution of Lorentzian and Gaussian components.

Relative intensity noise (RIN) is defined as the total quantity of photon noise within a given bandwidth.  Total noise from a laser typically includes shot noise, thermal/system noise, and light power (total photon energy per second) fluctuation.  The term RIN and excess photon noise have been often used interchangeably, although it is critical to differentiate the excess photon noise from other sources of noise in applications where excess photon noise is limiting the performance. Excess RIN is informally designated to differentiate such noise without contribution from shot noise and thermal noise.