The Q-Factor in Laser Frequency Noise

Q Definition
An optical resonator is a device that can trap light of specific wavelength (frequency). These frequencies are referred to as resonator modes. The Q factor (quality factor) of an optical resonator is a parameter that describes how the energy is trapped in the resonator, or equivalently, how long the energy can be stored in the resonator mode. Q is defined by the following equation:

- where ν is the optical frequency of the light and BW is the bandwidth of the resonator mode being considered. The larger the Q is at a specific optical frequency, the narrower the bandwidth, and the longer the energy can be stored in the resonator. The time constant of the “field” in the resonator, τ, is related to the BW and Q by:
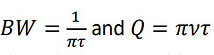
- respectively (n.b., if the time constant is defined by power as opposed to field, then there is an additional factor of 2 in these formulae).
OEwaves OE0200 Ultra-high Q (crystalline) resonators of are a special type, referred to as Whispering Gallery Mode (WGM) resonators. WGM’s are characterized by extremely high Qs, since the loss mechanisms in these resonators are determined by the transparency of the material (material loss), size of the diameter of the resonator (bending loss) and surface smoothness (scattering loss). Since all these losses can be made negligibly small, OE0200 Ultra-high Q resonators have an optical Q factor larger than 108 across a wide range of wavelengths from UV to mid-IR. At the standard telecom wavelength of 1550 nm (ν=193 THz), the BW of the resonator is less than 2 MHz, and as small as 100 kHz. The field time constant is longer than 0.16 μs for a resonator with a mode BW smaller than 2 MHz.
Why is an Ultra-high Q-factor important?
As can be seen in the above formulae, for a fixed optical frequency (wavelength), a larger Q factor results in a small bandwidth and long storage time of the optical power. These properties make the resonator very useful in the multiple applications.
Passive Filtering and Referencing
Since the optical resonator has a very small bandwidth, it can be used as a narrow bandpass filter to eliminate undesired optical fields in the spectrum. This property allows precise spectral measurement by using the cavity’s mode as an optical ruler for frequency calibration. Furthermore, the resonator can be further stabilized, such that external lasers or cavities can lock to it as a reference in a wide spectral range. These features are desirable in many applications requiring precise frequencies or low noise lasers, such as atomic clocks and quantum sensors. They are also used in applications where narrow filtering of a signal is required. An example is filtering of a large noise source close to a small signal. Such an optical filter can be used in RF applications when the RF signal is modulated on light and then filtered by introducing the light to a high Q resonator.
Narrow Linewidth Lasers
The narrow bandwidth resonator can be used as an ultra-narrow bandwidth “mirror” through Rayleigh scattering of light from the resonator material or any impurities within the resonator material. A laser with an intrinsic large frequency or phase noise will see feedback from light back scattered by the resonator, creating an “external cavity laser system”. The active lasing process will further suppress the linewidth of the laser far below the resonator bandwidth; this technique has been used in OEwaves’ proprietary laser design to achieve sub-Hertz instantaneous Lorentzian linewidth. Such narrow linewidth lasers are critical in many applications, including low-noise optical carriers in telecommunications, efficient sources for excitation of atomic or ionic transitions in quantum technology, or as long coherence length sources for LiDAR.
Nonlinear Optics
The higher the resonator Q, the longer optical energy can be stored in the resonator, i.e., optical circulation power is amplified in the resonator. This property creates low-threshold nonlinear optical effects with applications, such as:
- Frequency comb and soliton comb generation through four-wave-mixing
- Brillouin lasers and Raman lasers through phonon interactions
- Second harmonic generation and sum frequency generation via frequency conversion of photons
- Efficient pumping of rare Earth ions via ultra-high-Q solid-state lasers or amplifiers.
How is Q measured?
There are several ways to measure the Q factor of a resonator. Here, we introduce two methods: ringdown spectroscopy for measuring the Q factor of a resonator in time domain, and sideband spectroscopy for measuring the Q factor of a resonator in frequency domain.
1. Ring-Down Spectroscopy

Ring-down spectroscopy, in essence, measures the decay time of the stored optical field inside the resonator. This method treats the resonator like an “photon capacitor,” and the field starts to decay when the pump is removed. By measuring the time constant of the decay trace, the bandwidth, and therefore the quality factor, are calculated.
A system diagram and representative spectra are shown in Figure 1. The frequency of a probe laser is linearly swept across the mode of the resonator under test. Power is coupled into the resonator at the frequency of the mode; once the laser frequency is swept past the mode, the resonator starts to release the optical field stored inside. This resonator optical field interferes with the laser’s optical field at the photodiode, producing an oscillation which decays with the time constant of the resonator. This time constant is extracted to calculate Q.
2. Sideband Spectroscopy
Sideband spectroscopy, contrary to ringdown spectroscopy, measures the bandwidth of a resonator in the frequency domain. This method utilizes the sidebands of an optical mode to calibrate the oscilloscope, such that the bandwidth of the mode can be directly measured precisely. The resolution of this method is limited by the probe laser linewidth, the precision of the signal generator and oscilloscope, and drift of the resonator and laser. OEwaves’ Ultra-narrow Linewidth Lasers give the highest precision measurement using this technique.
.jpeg)
An example setup for sideband spectroscopy and the measured spectrum is shown in Figure 2. The freespectral-range (FSR) is defined by the frequency difference between the modes in the same mode family. Applying a fast modulation (f ~ FSR) on a linearly frequency swept laser. This fast modulation creates sidebands of the original mode and nearby modes. Since the modulation frequency is close to the FSR, the sidebands created by the m=±1 modes will be symmetric and very close to the target mode m=0, where m denotes the relative longitudinal mode number. The FSR is directly and precisely measured by overlapping the sidebands on top of the target mode by tuning f. Furthermore, using the f tuning to calibrate the oscilloscope, the BW of the target mode is measured, resulting in a precise measurement of Q.
%20(1).png)

%20(3).jpg)
%20(1).jpg)
.png)

